您的位置：首页 > 软件编程 > 其它相关  >  Matlab使用fft画出信号频谱图的方法

Matlab使用fft画出信号频谱图的方法

 更新时间：2021年5月19日 16:07  点击：2640

做雷原作业，需要对信号进行频谱分析，网上一搜太乱了，很多不是我想要的，特此整理。
DSP还没学到fft，就不对fft原理进行详细解释了，直接上代码。

fs=500;%采样率
f1=5;%信号频率
f2=10;%信号频率
T=1;%时宽1s
n=round(T*fs);%采样点个数
t=linspace(0,T,n);%时域横坐标
x = 3+cos(2*pi*f1*t) + 2.*cos(2*pi*f2*t);%形成三频信号,注意第二个频率信号幅度为2，直流幅度为3
figure(1);
plot(t,x);%画时域图
xlabel("t/s")
grid on

X = fftshift(fft(x./(n))); %用fft得出离散傅里叶变换
f=linspace(-fs/2,fs/2-1,n);%频域横坐标，注意奈奎斯特采样定理，最大原信号最大频率不超过采样频率的一半
figure(2)
plot(f,abs(X));%画双侧频谱幅度图
xlabel("f/Hz")
ylabel("幅度")
grid on

显然，该信号有三个频率分量，直流（0频），5Hz和10Hz，对应的幅度分别为3、1、2，其时域波形图如下:

在这里插入图片描述

转换为频域的关键函数是X = fftshift(fft(x./(n)));一定注意需要除以总样本数n，然后用fftshift将曲线挪一下位置。
做完这步操作后，得出的是双边频谱，频率范围从-fs/2到fs/2，这是因为奈奎斯特采样定理，给定采样频率为fs，那么原信号的最大频率不超过fs/2。横坐标的点数和时域信号的采样点数相同，这由离散傅里叶变换的性质给出。

绘制频谱幅度图如下：

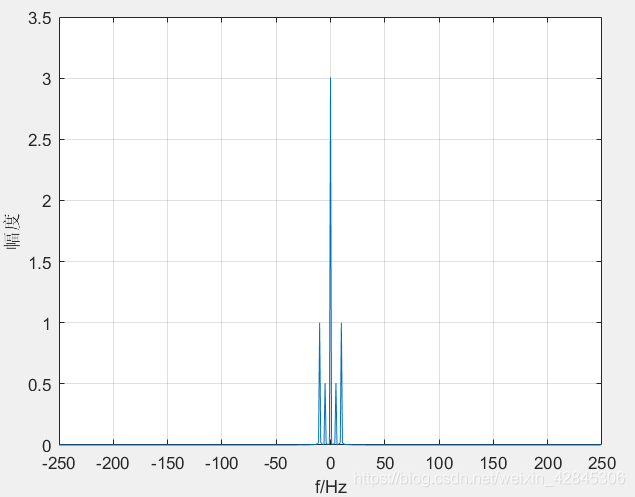
在这里插入图片描述

可以看到，直流分量的幅度是3，这与时域的幅度相同，5Hz和10Hz的幅度分别为0.5和1，这比时域的幅度减小了一半，这是由于这个频谱图是双边频谱。沿着x=0线“对折”过去加起来，就变成单边频谱，频域幅度就和时域幅度对应上了。

到此这篇关于Matlab使用fft画出信号频谱的文章就介绍到这了,更多相关Matlab画fft信号频谱内容请搜索猪先飞以前的文章或继续浏览下面的相关文章希望大家以后多多支持猪先飞！

[!--infotagslink--]

相关文章

  • 详解Matlab中 sort 函数用法

    这篇文章主要介绍了matlab中 sort 函数用法 的相关资料,需要的朋友可以参考下...2016-03-22

  • 如何用Matlab和Python读取Netcdf文件

    这篇文章主要介绍了如何用Matlab和Python读取Netcdf文件，帮助大家更好的理解和学习使用python，感兴趣的朋友可以了解下...2021-02-20

  • Matlab使用fft画出信号频谱图的方法

    这篇文章主要介绍了Matlab使用fft画出信号频谱图的方法,本文通过实例图文相结合给大家介绍的非常详细，对大家的学习或工作具有一定的参考借鉴价值，需要的朋友可以参考下...2021-05-19

  • 将pycharm配置为matlab或者spyder的用法说明

    这篇文章主要介绍了将pycharm配置为matlab或者spyder的用法说明，具有很好的参考价值，希望对大家有所帮助。一起跟随小编过来看看吧...2020-06-09

  • MATLAB 如何求取离散点的曲率最大值

    这篇文章主要介绍了MATLAB 求取离散点的曲率最大值操作，具有很好的参考价值，希望对大家有所帮助。一起跟随小编过来看看吧...2021-04-16

  • Matlab实现数据的动态显示方法

    这篇文章主要为大家详细介绍了Matlab使用Plot函数实现数据动态显示方法，具有一定的参考价值，感兴趣的小伙伴们可以参考一下...2020-04-25

  • 简述Matlab中size()函数的用法

    size（）函数用来获取矩阵的行数和列数。接下来通过本文给大家介绍matlab中size()函数的用法，需要的朋友一起学习吧...2016-03-22

  • Matlab制作视频并转换成gif动态图的两种方法

    这篇文章主要介绍了Matlab制作视频并转换成gif动态图的两种方法,第一种方法使用movie（f）直接取生成AVI视频文件，相对来说比较简单，需要的朋友可以参考下...2020-04-25

  • MATLAB Delaunay算法提取离散点边界的方法

    这篇文章主要为大家详细介绍了MATLAB Delaunay算法提取离散点边界的方法，具有一定的参考价值，感兴趣的小伙伴们可以参考一下...2020-04-25

  • C++如何调用matlab函数

    这篇文章主要介绍了C++如何调用matlab函数的相关资料,非常不错，具有参考借鉴价值，需要的朋友可以参考下...2020-04-25

  • 基于python实现matlab filter函数过程详解

    这篇文章主要介绍了基于python实现matlab filter函数过程详解,文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下...2020-06-09

  • C#调用Matlab生成的dll方法的详细说明

    这篇文章详细介绍了C#调用Matlab生成的dll方法，有需要的朋友可以参考一下...2020-06-25

  • 解决python调用matlab时的一些常见问题

    这篇文章主要介绍了解决python调用matlab时的一些常见问题，具有很好的参考价值，希望对大家有所帮助。一起跟随小编过来看看吧...2021-03-24

  • C++调用Matlab函数求特征值

    这篇文章主要为大家详细介绍了C++调用Matlab函数求特征值，具有一定的参考价值，感兴趣的小伙伴们可以参考一下...2020-04-25

  • Java如何调用Matlab程序

    这篇文章主要介绍了Java如何调用Matlab程序的操作，具有很好的参考价值，希望对大家有所帮助。如有错误或未考虑完全的地方，望不吝赐教...2021-09-06

  • matlab、python中矩阵的互相导入导出方式

    这篇文章主要介绍了matlab、python中矩阵的互相导入导出方式，具有很好的参考价值，希望对大家有所帮助。一起跟随小编过来看看吧...2020-06-02

  • WPF调用Matlab函数的方法

    这篇文章主要为大家详细介绍了WPF调用Matlab函数的方法,具有一定的参考价值，感兴趣的小伙伴们可以参考一下...2020-06-25

  • 解析在main函数之前调用函数以及对设计的作用详解

    本篇文章是对在main函数之前调用函数以及对设计的作用进行了详细的分析介绍，需要的朋友参考下...2020-04-25

  • 基于MATLAB神经网络图像识别的高识别率代码

    今天小编就为大家分享一篇关于基于MATLAB神经网络图像识别的高识别率代码，小编觉得内容挺不错的，现在分享给大家，具有很好的参考价值，需要的朋友一起跟随小编来看看吧...2020-04-25

  • MATLAB实现五子棋游戏（双人对战、可悔棋）

    这篇文章主要为大家详细介绍了MATLAB实现五子棋游戏，可以进行双人对战、也可悔棋，具有一定的参考价值，感兴趣的小伙伴们可以参考一下...2020-04-25